가중치 그래프란(Weighted Graph)
- 네트워크(network)라고도 함
- 간선에 가중치가 할당된 그래프
- 비용(cost)
- 가중치(weight)
- 길이(length)

- 예
- 정점 : 각 도시를 의미
- 간선 : 도시를 연결하는 도로 의미
- 가중치 : 도로의 길이
가중치 표현 방법
- 인접 행렬 M[i][j]를 가중치를 위해 사용
- 추가적인 메모리 사용 없이 가중치 표현 가능
- 인접행렬M을 이용한 그래프 표현에서 M[i][j]가 간선 (i,j)의 가중치 값을 나타냄
- 만약, 간선(i,j)가 존재하지 않으면? -> M[i][j]가 매우 큰 값을 갖도록 함

최단 경로
- 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로
- 간선의 가중치는 비용, 거리, 시간 등
Qusetion. A에서 D까지의 최단 경로는?
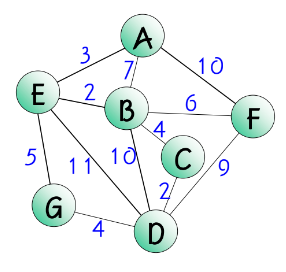
다익스트라(Dijkstra) 알고리즘
- 시작 정점 v에서 모든 다른 정점까지의 최단 경로 찾는 대표적인 최단 경로 탐색 알고리즘
- 모든 간선이 양인 값을 가질 때 사용
- 인공위성 GPS 소프트웨어, 내비게이션 등에 가장 많이 사용됨
- 매 상황에서 가장 비용이 적은 노드를 선택
탐욕(greedy) 알고리즘
여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없음
-> 탐욕 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로는 최적인 문제들
시작 정점 A에서 모든 다른 정점까지의 최단 경로를 찾는 과정
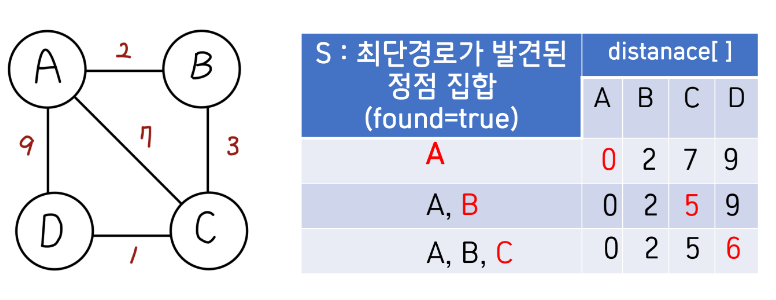
distance값 갱신
- 새로운 정점이 S에 추가되면 distance값 갱신
dist[w] = min(dist[w], dist[u]+weight[u][w]) //둘중에 작은것
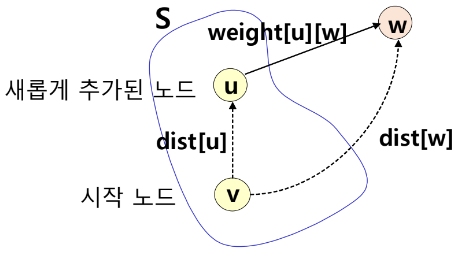
최단경로 증명

- distance 값이 가장 작은 정점이 u
- v에서 u까지의 최단경로는 ①
- 경로 ②는 ①보다 항상 길 수밖에 없음
- Why? ③은 항상 양수이므로!
- 따라서 매 단계에서 distance 값이 가장 작은 정점들을 추가하면 모든 정점까지의 최단거리를 구할 수 있다
dijikstra(v)
found[v] ← true // S 집합에 넣기
dist[v] ← 0
for 그래프에 존재하는 정점 w do
dist[w] ← weight[v][w]
while 모든 정점의 최단 경로 발견할 때까지
u ← 집합 S에 속하지 않는 정점 중에서 최소 distance 정점; dist에서 가장 작은 정점 선택
found[u] ← true dist 값 갱신
for u에 인접하고 S에 있지 않은 각 정점 z do
if dist[u]+weight[u][z] < dist[z]
then dist[z]←dist[u]+weight[u][z]
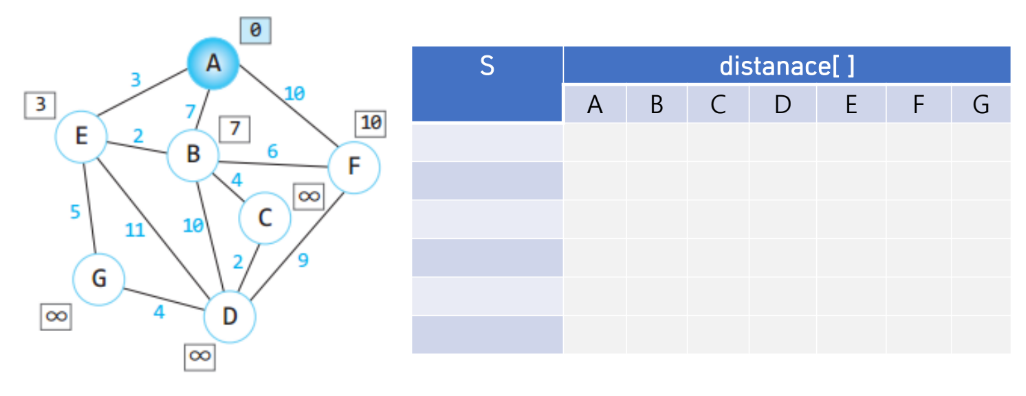
연습문제(1)
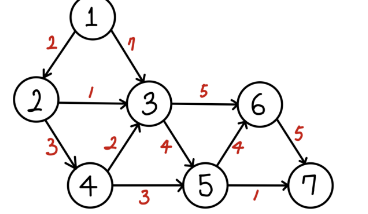

연습문제(2)
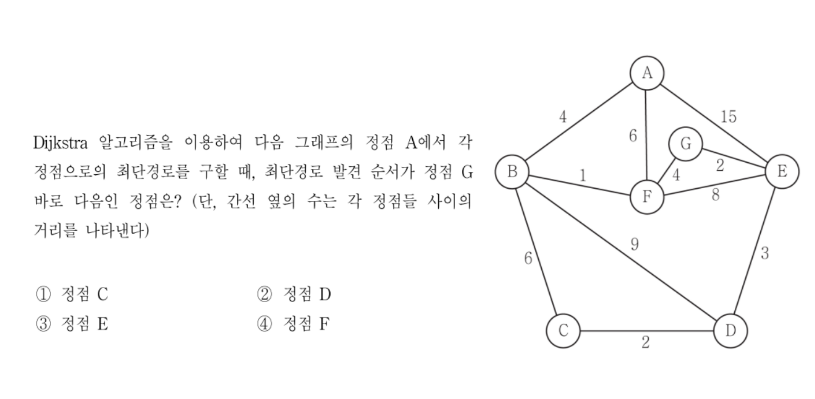
QUIZ1. 2020 7급 서울시 공무원 문제

QUIZ 2.
최단 경로 탐색 알고리즘
- 단일 출발점 최단 경로 : 다익스트라 알고리즘, 벨만 포드 알고리즘
- 모든 출발점 최단 경로 : 플로이드 알고리즘
- 다익스트라 알고리즘은 벨만 포드 알고리즘에 비해 실행 속도가 더 빠름
- 다익스트라는 가중치가 양수일 때만 실행할 수 있고 가중치가 음수일 때는 벨만 포드 알고리즘 사용
실습1 : 다익스트라 알고리즘 구현하기
n개의 정점이 존재하고 m개의 간선의 양 끝 정점과 가중치가 주어질 때,1번 정점에서 다른 모든 정점으로 가는 최다 ㄴ경로를 구하는 프로그램을 작성해보세요. 이때 주어지는 그래프는 단방향 그래프입니다.

STEP1 : 입력, 자료구조 셋팅
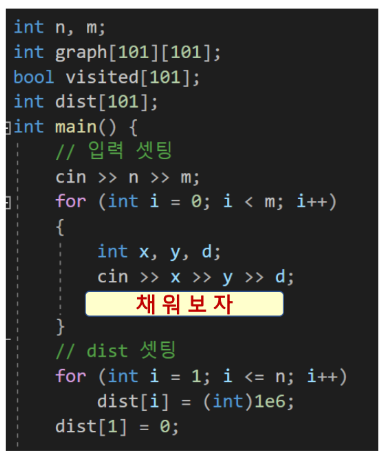
STEP2 : dist 값 갱신
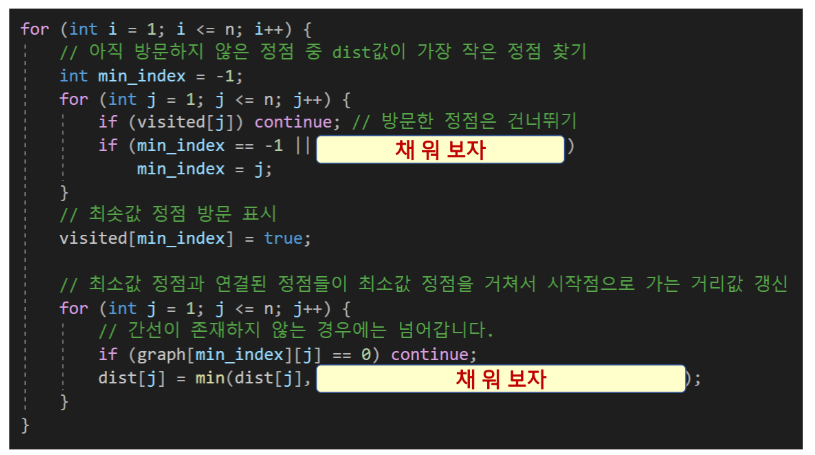
STEP3 : 출력

완성코드
#include <iostream>
#include <vector>
#include <tuple> //
using namespace std;
int n, m; // n: 정점개수, m: 간선 개수
int graph[101][101];// 인접 행렬, 최대 100개의 정점에 대해 각 정점 사이의 거리를 저장
bool visited[101]; // 방문 여부를 기록하는 배열
int dist[101]; // 시작점으로부터 각 정점까지의 최단 거리를 저장하는 배열, 초기값 1e6
int main() {
// 입력 셋팅
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int x, y, d;
cin >> x >> y >> d;
graph[x][y] = d;
}
// dist 셋팅
for (int i = 1; i <= n; i++)
dist[i] = (int)1e6;
dist[1] = 0; //시작점(여기서는 1번 정점)의 거리는 0으로 설정하여, 그 자신까지의 거리가 0임을 나타냄.
for (int i = 1; i <= n; i++) {
// 아직 방문하지 않은 정점 중 dist값이 가장 작은 정점 찾기
int min_index = -1; // 초기 값으로, 아직 최소값을 찾지 못했을 때 설정
for (int j = 1; j <= n; j++) {
if (visited[j]) continue; // 방문한 정점은 건너뛰기
if (min_index == -1 || dist[min_index] > dist[j]) // 더 작은 거리를 가진 정점을 발견하면, 그 정점으로 min_index를 업데이트합니다.
min_index = j;
}
// 최솟값 정점 방문 표시
visited[min_index] = true; //min_index로 선택된 정점을 방문 처리(visited[min_index] = true)한다.
// 최소값 정점과 연결된 정점들이 최소값 정점을 거쳐서 시작점으로 가는 거리값 갱신
for (int j = 1; j <= n; j++) {
// 간선이 존재하지 않는 경우에는 넘어갑니다.
if (graph[min_index][j] == 0) continue;
dist[j] = min(dist[j], dist[min_index] + graph[min_index][j]);
//min_index 정점에서 갈 수 있는 모든 다른 정점들에 대해, 그 정점을 거쳐 가는 경로가 더 짧은 경우에는 dist[j] 값을 갱신한다
}
}
// 시작점(1번 정점)으로부터 각 지점까지의 최단거리 값을 출력
for (int i = 2; i <= n; i++) {
// 연결되어 있지 않은 정점은 -1 출력
if (dist[i] == (int)1e6) cout << -1 << endl;
else cout << dist[i] << endl;
}
return 0;
}
개선된 다익스트라 알고리즘의 시간 복잡도
- 다익스트라 알고리즘을 진행하면 각 간선을 한 번씩 보게 되는데, 이때 dist값이 변하면 우선순위큐에서의 순서가 계속 바뀌게 될 수도 있으므로 시간복잡도는 간선의 수 x 우선순위 큐 시간 복잡도
- -> 그래프 내의 정점의 수를 V, 간선의 수를 E라 했을 때 시간 복잡도는 O(E log V)
'프로그래밍 언어 > C++' 카테고리의 다른 글
| [코드트리 조별과제] 2024-08-05 2문제 풀이 (0) | 2024.08.11 |
|---|
가중치 그래프란(Weighted Graph)
- 네트워크(network)라고도 함
- 간선에 가중치가 할당된 그래프
- 비용(cost)
- 가중치(weight)
- 길이(length)

- 예
- 정점 : 각 도시를 의미
- 간선 : 도시를 연결하는 도로 의미
- 가중치 : 도로의 길이
가중치 표현 방법
- 인접 행렬 M[i][j]를 가중치를 위해 사용
- 추가적인 메모리 사용 없이 가중치 표현 가능
- 인접행렬M을 이용한 그래프 표현에서 M[i][j]가 간선 (i,j)의 가중치 값을 나타냄
- 만약, 간선(i,j)가 존재하지 않으면? -> M[i][j]가 매우 큰 값을 갖도록 함

최단 경로
- 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로
- 간선의 가중치는 비용, 거리, 시간 등
Qusetion. A에서 D까지의 최단 경로는?

다익스트라(Dijkstra) 알고리즘
- 시작 정점 v에서 모든 다른 정점까지의 최단 경로 찾는 대표적인 최단 경로 탐색 알고리즘
- 모든 간선이 양인 값을 가질 때 사용
- 인공위성 GPS 소프트웨어, 내비게이션 등에 가장 많이 사용됨
- 매 상황에서 가장 비용이 적은 노드를 선택
탐욕(greedy) 알고리즘
여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없음
-> 탐욕 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로는 최적인 문제들
시작 정점 A에서 모든 다른 정점까지의 최단 경로를 찾는 과정

distance값 갱신
- 새로운 정점이 S에 추가되면 distance값 갱신
dist[w] = min(dist[w], dist[u]+weight[u][w]) //둘중에 작은것

최단경로 증명

- distance 값이 가장 작은 정점이 u
- v에서 u까지의 최단경로는 ①
- 경로 ②는 ①보다 항상 길 수밖에 없음
- Why? ③은 항상 양수이므로!
- 따라서 매 단계에서 distance 값이 가장 작은 정점들을 추가하면 모든 정점까지의 최단거리를 구할 수 있다
dijikstra(v)
found[v] ← true // S 집합에 넣기
dist[v] ← 0
for 그래프에 존재하는 정점 w do
dist[w] ← weight[v][w]
while 모든 정점의 최단 경로 발견할 때까지
u ← 집합 S에 속하지 않는 정점 중에서 최소 distance 정점; dist에서 가장 작은 정점 선택
found[u] ← true dist 값 갱신
for u에 인접하고 S에 있지 않은 각 정점 z do
if dist[u]+weight[u][z] < dist[z]
then dist[z]←dist[u]+weight[u][z]
연습문제(1)


연습문제(2)

QUIZ1. 2020 7급 서울시 공무원 문제

QUIZ 2.

최단 경로 탐색 알고리즘
- 단일 출발점 최단 경로 : 다익스트라 알고리즘, 벨만 포드 알고리즘
- 모든 출발점 최단 경로 : 플로이드 알고리즘
- 다익스트라 알고리즘은 벨만 포드 알고리즘에 비해 실행 속도가 더 빠름
- 다익스트라는 가중치가 양수일 때만 실행할 수 있고 가중치가 음수일 때는 벨만 포드 알고리즘 사용
실습1 : 다익스트라 알고리즘 구현하기
n개의 정점이 존재하고 m개의 간선의 양 끝 정점과 가중치가 주어질 때,1번 정점에서 다른 모든 정점으로 가는 최다 ㄴ경로를 구하는 프로그램을 작성해보세요. 이때 주어지는 그래프는 단방향 그래프입니다.

STEP1 : 입력, 자료구조 셋팅

STEP2 : dist 값 갱신

STEP3 : 출력

완성코드
#include <iostream>
#include <vector>
#include <tuple> //
using namespace std;
int n, m; // n: 정점개수, m: 간선 개수
int graph[101][101];// 인접 행렬, 최대 100개의 정점에 대해 각 정점 사이의 거리를 저장
bool visited[101]; // 방문 여부를 기록하는 배열
int dist[101]; // 시작점으로부터 각 정점까지의 최단 거리를 저장하는 배열, 초기값 1e6
int main() {
// 입력 셋팅
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int x, y, d;
cin >> x >> y >> d;
graph[x][y] = d;
}
// dist 셋팅
for (int i = 1; i <= n; i++)
dist[i] = (int)1e6;
dist[1] = 0; //시작점(여기서는 1번 정점)의 거리는 0으로 설정하여, 그 자신까지의 거리가 0임을 나타냄.
for (int i = 1; i <= n; i++) {
// 아직 방문하지 않은 정점 중 dist값이 가장 작은 정점 찾기
int min_index = -1; // 초기 값으로, 아직 최소값을 찾지 못했을 때 설정
for (int j = 1; j <= n; j++) {
if (visited[j]) continue; // 방문한 정점은 건너뛰기
if (min_index == -1 || dist[min_index] > dist[j]) // 더 작은 거리를 가진 정점을 발견하면, 그 정점으로 min_index를 업데이트합니다.
min_index = j;
}
// 최솟값 정점 방문 표시
visited[min_index] = true; //min_index로 선택된 정점을 방문 처리(visited[min_index] = true)한다.
// 최소값 정점과 연결된 정점들이 최소값 정점을 거쳐서 시작점으로 가는 거리값 갱신
for (int j = 1; j <= n; j++) {
// 간선이 존재하지 않는 경우에는 넘어갑니다.
if (graph[min_index][j] == 0) continue;
dist[j] = min(dist[j], dist[min_index] + graph[min_index][j]);
//min_index 정점에서 갈 수 있는 모든 다른 정점들에 대해, 그 정점을 거쳐 가는 경로가 더 짧은 경우에는 dist[j] 값을 갱신한다
}
}
// 시작점(1번 정점)으로부터 각 지점까지의 최단거리 값을 출력
for (int i = 2; i <= n; i++) {
// 연결되어 있지 않은 정점은 -1 출력
if (dist[i] == (int)1e6) cout << -1 << endl;
else cout << dist[i] << endl;
}
return 0;
}
개선된 다익스트라 알고리즘의 시간 복잡도
- 다익스트라 알고리즘을 진행하면 각 간선을 한 번씩 보게 되는데, 이때 dist값이 변하면 우선순위큐에서의 순서가 계속 바뀌게 될 수도 있으므로 시간복잡도는 간선의 수 x 우선순위 큐 시간 복잡도
- -> 그래프 내의 정점의 수를 V, 간선의 수를 E라 했을 때 시간 복잡도는 O(E log V)
'프로그래밍 언어 > C++' 카테고리의 다른 글
| [코드트리 조별과제] 2024-08-05 2문제 풀이 (0) | 2024.08.11 |
|---|
